それではヒストリカルボラティリティの算出方法を説明します。

今回は個人投資家に人気の、
南アフリカランド/円のHVを算出したいと思います。

算出方法と言っても、
実はエクセルに計算してもらいますので、
ものすごく簡単です。

ミルクティーでも用意しながらリラックスして読んでください！（笑）

データを取得します。

まず以下のサイトからデータを取得します。

http://www.oanda.com/convert/fxhistory

このサイトでは、期間と通貨ペアを指定すれば、
その期間中の買値と売値、中点の指定した為替レートが取得できます。

今回は、
2002年3月4日から2007年3月4日のデータを取得したいと思います。
（日付けは古いですが、計算方法自体は陳腐化していませんので、
2017年12月6日現在でも全く同じ手順で進めて下さい。）

南アフリカランド/円の通貨ペアの為替履歴を見るので、
手元にある通貨:を南アフリカランド　ZARを、
必要な通貨:にJPYを指定します。

期間は、2002 3月4日から2007 3月4日まで、としたいところですが、
取得期間を1年より長くしてしまうと、うまいことデータを取得できないので、

・2002 3月4日から2003 3月3日まで
・2003 3月4日から2004 3月3日まで
・2004 3月4日から2005 3月3日まで
・2005 3月4日から2006 3月3日まで
・2006 3月4日から2007 3月2日まで
・2007 3月3日から2007 3月4日まで

のように6回に分けて取得する必要があります、、

ヒストリカルボラティリティは正確なレートデータが多いほど良いので、
面倒だなぁと思いますが、現状6回に分けて取るしかなさそうです。

そして、右上にある「ダウンロード」をクリックすれば、
CSV形式で実際に取得することが出来ます。

エクセルでCSVデータを開くと、一部文字化けしてるところがあります。
特に気にする必要はありません。

まず6つのCSVファイルにある日付と為替データを、
順番を気にせずに1つのエクセルファイルにコピペします。

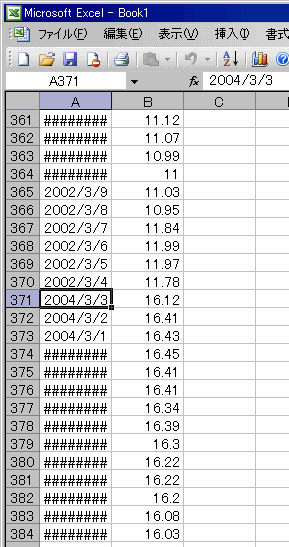
もちろん日付の順番がバラバラだとダメなので、
古い日付からの順番になるように並び替える作業が必要です。

日付が記入されているセルを選択して、
メニューにある「データ」→「並び替え」をクリックし、
昇順にチェックが入っていることを確認してからOKをクリックすると、
2002年3月4日から2007年3月4日と古い日付順に並び替わります。

とりあえず為替レートのデータだけが必要なので、
日付が記入されているA列のセルを削除しちゃいましょう。

前日比を計算します。

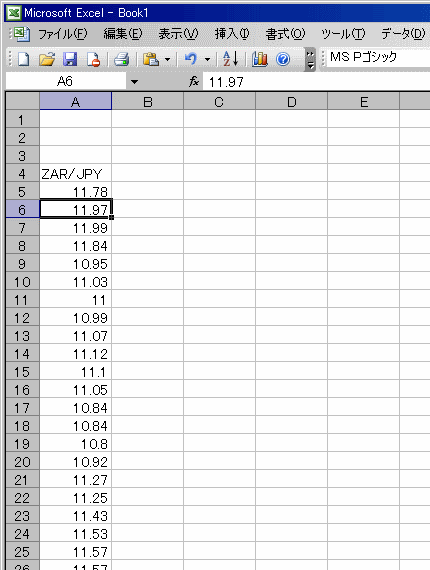
ヒストリカルボラティリティの算出には、レートそのものではなく、前日比を利用します。

今回のデータは、下に行くほど新しいデータになっているので、
一番上のデータをA6/A5として、これを一番下までコピーします。

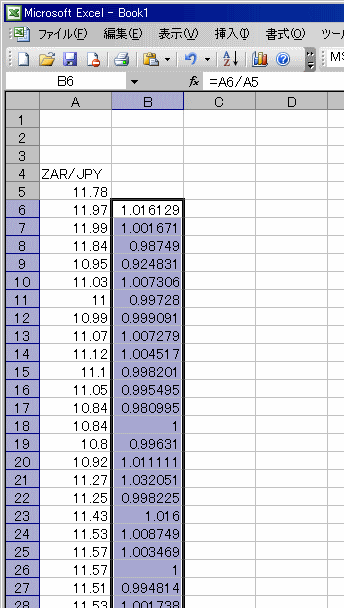
「当日÷前日」とすることによって、
その日が前日に比べてどれくらい上昇または下降したのかが、
率で算出されます。

ヒストリカルボラティリティを算出します。

STDEVP関数を使って、ヒストリカルボラティリティを計算します。

この関数はSTDEVP()の()の中に入れた集団（数字の集まり）の、
標準偏差を求める関数です。

標準偏差は、為替ではヒストリカルボラティリティのことだと思ってください。

ですので、この関数の括弧の中に、
今回算出した2002年3月4日から2007年3月4日までの前日比を全て入れれば、
ヒストリカルボラティリティが算出されることになります。

「ZAR/JPY」や「前日比」のセルの色付けなどは、
好みで見やすくしてください。

STDEVP関数の()内は、
前日比の最初（B6）から最後（B1831）を指定します。

これをパーセント表示にすれば、
1日あたりのHVが算出されます。

しかし、通常リターンである金利は、
年利で考えますので、HVも年換算します。

統計学では年間の営業日には250日（または260日）を使うのが普通です。

ヒストリカルボラティリティの場合、
「250の平方根」をかければ年換算されることになります。

これをエクセルで計算するには、

=STDEVP(B6:B1831)*SQRT(250)

と入力します。

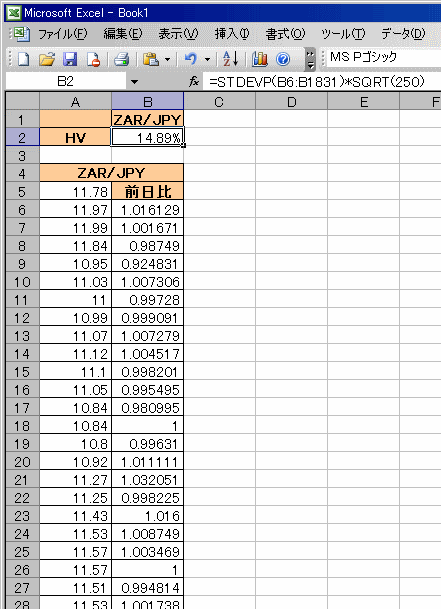
以上でヒストリカルボラティリティの算出は完了です。

セルをパーセント表示にするには、
パーセント表示するセルを選択して、ツールバーの「％」マークをクリックするか、
右クリックして「セルの書式設定」から「表示形式」のタブを開いて、
「パーセンテージ」を選択して「OK」をクリックします。

セルの書式設定を開く方が、
小数点以下の桁数まで指定できるので、いいかもしれません。

ZAR/JPYのHVは14.89%となりますが、
これはかなり大きな変動率になります。

こうやって出したHVには、以下のことが言えます。

・年間±14.89%の範囲内に68.3%の確率で収まる
・年間±29.78%の範囲内に95.4%の確率で収まる

この確率は統計学上そうなっていると覚えておくといいと思います。

収まる確率（68.3%、95.4%）は、為替に限らず、
どんなデータを入れても、同じになります。

HVが大きい通貨は、
スワップ派にとってはそれだけリスクが大きい通貨だということになります。

このようにして通貨ペアのHVが計算できれば、
その通貨の金利がリスクにみあっているかを数値で確認することができます。

ただ、HVはその名前のとおり、
過去のデータから未来を予測するものですから、
必ず今後もこのボラティリティになるということではありません。

歴史上起こらなかったような事件が起きれば、
統計学的にもほとんど起こりえない確率の変動幅になることもあります。

今回紹介した算出方法で出した各通貨のHVを、
「ヒストリカルボラティリティ比較表」に掲載しています。

どうしても算出方法が難しい！という人は、
メインの通貨のHVはここを参照してもらえればと思います。